【学习笔记】LGV引理

Posted on 2022-01-15 Edited on 2022-02-24

本来没打算写的, 但是感觉老容易忘, 就还是写一下吧.

LGV 引理(Lindstrom-Gessel-Viennot lemma)

本文主要写对引理的阐述和证明.

LGV 引理内容

$G$ 是一个有限的带权有向无环图, 即每个顶点度是有限的, 不存在有向环(所以路径数是有限的).
起点 $A = \{a_1,\dots,a_n\}$ , 终点 $B = \{b_1,\dots,b_n\}$ .
每条边 $e$ 有边权 $w_e$ , 并假定属于某个交换环.
对于一个有向路径 $P$ , 定义 $\omega(P)$ 为路径上所有边权的积.
对任意定点 $a,b$ , 定义 $e(a,b) = \sum\limits_{P : a \rightarrow b}{\omega(P)}$ .

设矩阵

$M = \left[\begin{array}{cccc} e(a_1,b_1) & e(a_1,b_2) & \cdots & e(a_1,b_n) \\ e(a_2,b_1) & e(a_2,b_2) & \cdots & e(a_2,b_n) \\ \vdots & \vdots & \ddots & \vdots \\ e(a_n,b_1) & e(a_n,b_2) & \cdots & e(a_n,b_n) \end{array}\right]$

从 $A$ 到 $B$ 的不相交路径 $P = (P_1,P_2,\dots,P_n)$ , $P_i$ 表示从 $a_i$ 到 $b_{\sigma(i)}$ 的一条路径, 其中 $\sigma$ 是一个排列(置换), 并且满足对任意 $i \not = j$ , $P_i$ 与 $P_j$ 没有公共点. 记 $\sigma(P)$ 表示 $P$ 对应的排列.

引理说明, $M$ 的行列式是所有从 $A$ 到 $B$ 的不相交路径 $P = (P_1,P_2,\dots,P_n)$ 的带符号和. 其中符号指 $\sigma(P)$ 的逆序数的奇偶性, 即 $(-1)^{逆序数}$ , 记为 $\operatorname{sign}(\sigma(P))$ .

$\operatorname{det}(M) = \sum_{P: A \rightarrow B}{\operatorname{sign}(\sigma(P)) \prod_{i=1}^n{\omega(P_i)}}$

证明

对一组路径 $P$ , 若对任意 $i \not = j$ , $P_i$ 与 $P_j$ 无公共点, 则称 $P$ 是一组不相交路径, 否则为一组相交路径. 为了简便, 以下记相交路径为 $P^c$ , 不相交路径为 $P^u$ . 不做特殊说明时, $P$ 为一组平凡路径. 当带下表时, 指一条路径. 定义 $\omega(P) = \omega(P_1)\omega(P_2)\cdots \omega(P_n)$ .

根据定义,

$\operatorname{det}(M) = \sum_{\sigma \in S_n}{\operatorname{sign}(\sigma)\prod_{i=1}^n{e(a_i,b_{\sigma(i)})}} \\ = \sum_{\sigma \in S_n}{\operatorname{sign}(\sigma) \prod_{i=1}^n{\sum_{P_i : a_i \rightarrow b_{\sigma(i)}}{\omega(P_i)}}}$

$\prod\limits_{i=1}^n{\sum\limits_{P_i : a_i \rightarrow b_{\sigma(i)}}{\omega(P_i)}}$ 展开后对应所有排列为 $\sigma$ 的路径组 $P$ ,

$\operatorname{det}(M) = \sum_{\sigma \in S_n}{\operatorname{sign}(\sigma)\sum_{P:(a_1,\dots,a_n) \rightarrow (b_{\sigma(1)},\dots,b_{\sigma(n)})}{\omega(P)}} \\ = \sum_{P:A \rightarrow B}{\operatorname{sign}(\sigma(P)) \omega(P)}$

现在形式已经相同, 只是 $P$ 的含义不同.

$\operatorname{det}(M) = \sum_{P^u:A \rightarrow B}{\operatorname{sign}(\sigma(P^u)) \omega(P^u)}+\sum_{P^c:A \rightarrow B}{\operatorname{sign}(\sigma(P^c)) \omega(P^c)}$

故若引理成立, 则必有 $\sum\limits_{P^c:A \rightarrow B}{\operatorname{sign}(\sigma(P^c)) \omega(P^c)} = 0$ .

设 $C$ 为所有 $P^c$ 构成的集合. 如果我们能构造一个双射关系 $f: C \rightarrow C$ , 满足对任意 $P^c \in C$ , $\omega(f(P^c)) = \omega(P^c)$ , $\operatorname{sign}(\sigma(f(P^c))) = -\operatorname{sign}(\sigma(P^c))$ .

$\sum_{P^c:A \rightarrow B}{\operatorname{sign}(\sigma(P^c)) \omega(P^c)} = \sum_{P^c:A \rightarrow B}{\operatorname{sign}(\sigma(f(P^c))) \omega(f(P^c))} \\ \sum_{P^c:A \rightarrow B}{\operatorname{sign}(\sigma(P^c)) \omega(P^c)} = \frac{1}{2}\sum_{P^c:A \rightarrow B}{\operatorname{sign}(\sigma(P^c)) \omega(P^c)}+\frac{1}{2}\sum_{P^c:A \rightarrow B}{\operatorname{sign}(\sigma(f(P^c))) \omega(f(P^c))} \\ = \frac{1}{2}\sum_{P^c:A \rightarrow B}{\operatorname{sign}(\sigma(P^c)) \omega(P^c)}+\frac{1}{2}\sum_{P^c:A \rightarrow B}{-\operatorname{sign}(\sigma(P^c)) \omega(P^c)} \\ = 0$

确实可以构造:

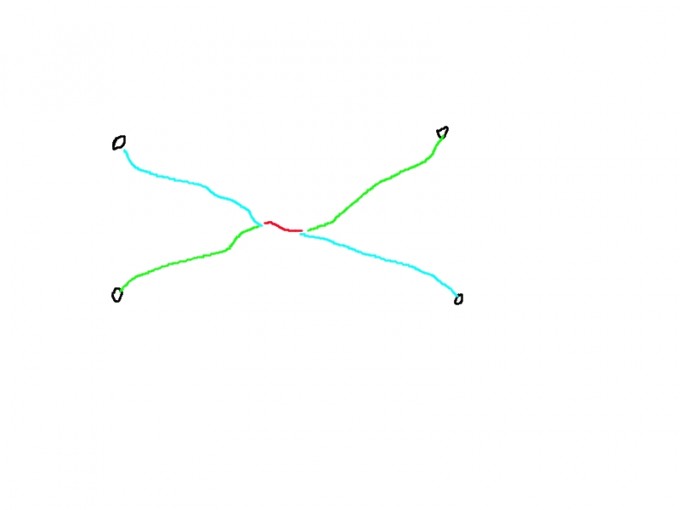
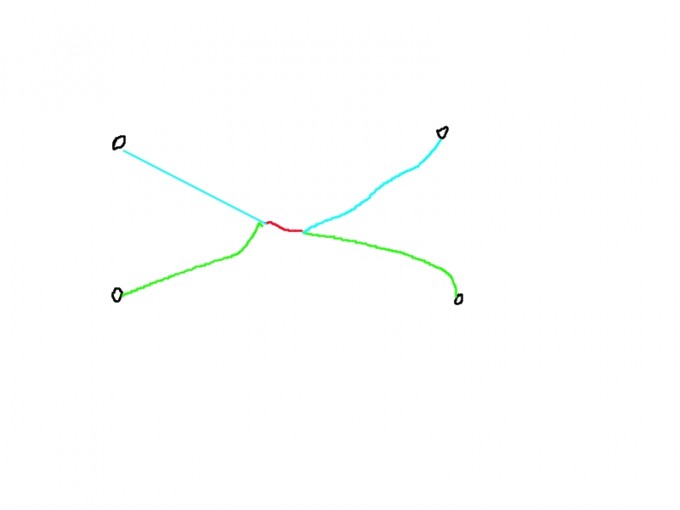
考虑 $P = (P_1,P_2,\dots,P_n)$ , $P \in C$ , 中找到最小的二元组 $(i,j)$ 满足 $P_i$ 和 $P_j$ 有交, 将相交之后的路径交换一下, 交换后得到 $P’$ . 显然有 $P’ \in C, P’ \not = P$ .