【学习笔记】矩阵树定理

Posted on 2021-11-05 Edited on 2022-02-24

矩阵树定理是利用矩阵行列式计算图的生成树个数的一个定理.

定义

首先讨论无向图 $G = \left( V,E \right)$ (允许重边, 不允许自环). 定义其度数矩阵 $D(G)$ 为

$D_{i,i}(G)=\deg(v_i),\quad D_{i,j}(G)=0\;\;(i\neq j)$

定义其邻接矩阵 $A(G)$ 为

$A_{i,j}(G)=\# \{e\in E(G)\;|\;e=(v_i,v_j)\}$

将 $G$ 的每条边任意指定一个方向, 定义 $G$ 的关联矩阵 (Incidence matrix) $M(G)$ ($M$ 是 $|V|\times|E|$ 的矩阵)为:

$M_{i,j}= \begin{cases} -1,\quad \ \ & v_i \text{是} e_j \text{的起点} \\ 1,\quad \ \ & v_i \text{是} e_j \text{的终点} \\ 0,\quad \ \ & otherwise \end{cases}$

定义 $G$ 的拉普拉斯矩阵 (Laplace matrix) $L(G)$ 为

$L(G)=D(G)-A(G)$

也可以形象的表示为

$L_{i,j} = \begin{cases} -m_{i,j},\quad \ \ & i \not= j,v_i \text{和},v_j \text{之间有} m_{i,j} \text{条边} \\ \operatorname{deg}(v_i),\quad \ \ & i = j \end{cases}$

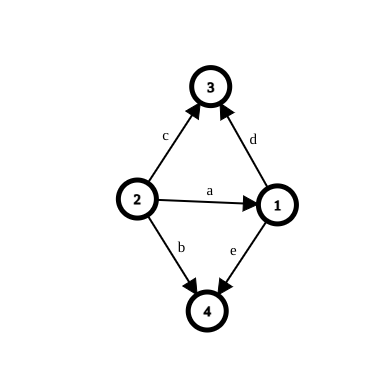
举例

上图的关联矩阵 $M$ 和拉普拉斯矩阵 $L$ 分别是:

$M = \left[\begin{array}{cccc} 1& 0& 0& -1& -1\\ -1& -1& -1& 0& 0\\ 0& 0& 1& 1& 0\\ 0& 1& 0& 0& 1 \end{array}\right], L = \left[\begin{array}{cccc} 3& -1& -1& -1\\ -1& 3& -1& -1\\ -1& -1& 2& 0\\ -1& -1& 0& 2 \end{array}\right]$

容易发现 $L$ 是对称的.实际上非主对角线上的元素也可以不是 $-1$ ,因为图 $G$ 允许重边存在.

几条引理

Lemma1: $MM^T = L$ ,其中 $M^T$ 表示 $M$ 的转置.

证明:

$(MM^T)_{i,j} = \sum_{e_k \in E}{M_{i,k}M^T_{k,j}} = \sum_{e_k \in E}{M_{i,k}M_{j,k}}$

然后分情况讨论.
当 $i \not= j$时,当且仅当存在一条边 $e_k \in E$ 把 $v_i,v_j$ 连起来时, $M_{i,k}M_{j,k} = -1$ ,其余情况 $M_{i,k}M_{j,k} = 0$ ,因此结果就是 $v_i,v_j$ 之间的边数.

当 $i = j$ 时,当且仅当存在一条边 $e_k \in E$ 的一端是 $v_i$ 时, $M_{i,k}M_{j,k} = 1$ ,因此结果就是它的度.

接下来我们定义一些 $M$ 的子矩阵,它们是证明的关键.

Def1 $reduced$ $incidence$ $matrix$ (笑死，根本不会英文翻译，姑且叫它关联减矩阵吧。。。) $M_0$ 是去掉 $M$ 最后一行得到的 $(p-1) \times q$ 的矩阵.

Def2 在此基础上定义一个 $(p-1) \times (p-1)$ 的矩阵 $M_0[S]$ ,其中集合 $S = \{ i_1,i_2,i_3, \dots,i_{p-1} \} \subseteq \{ 1,2,3,\dots,q \}$ .它的意思是,抽出矩阵 $M_0$ 的第 $i_1,i_2,\dots,i_{p-1}$ 列,得到一个新的矩阵，称之为 $M_0[S]$ .

$S$ 中的每个元素 $i_k$ 都和一条边的 $e_k$ 对应,所以为了方便,以下不区分 $S$ 和它所一一对应的边集.

接下来证明引理2

Lemma2 令 $S$ 为边集 $E$ 的一个大小为 $p-1$ 的子集,若 $G’ = \left( V,S \right)$ 不构成生成树,则 $\operatorname{det}(M_0[S]) = 0$ ;若构成生成树,则 $\operatorname{det}(M_0[S]) = \pm1$.

证明:

若 $G’$ 不构成生成树,则 $G’$ 包含圈 $C$ .设 $C$ 是由 $e_1,e_2,e_3,\dots,e_k$ ,共 $k$ 条边构成,那么容易证明矩阵 $M_0[S]$ 中, $i_1,i_2,i_3,\dots,i_k$ 这 $k$ 列线性相关(证明过程类似向量合成的感觉,就矩阵而言会更直观),故 $\operatorname{det}(M_0[S]) = 0$ .

补充:线性相关就是各行或列能互相线性表示,能进行初等变换,把某一行或列变换到另一行或列,最后有一行会全为 $0$ ,计算时行列式就等于 $0$ .所以行列式等于 $0$ 就是线性相关.相反的,线性无关它的行列式不等于 $0$ ,说明是满秩,没有一行或一列全为 $0$ .

若 $G’$ 构成生成树,则我们可以把 $G’$ 中的点进行排序(实际是拓扑排序),排成 $v_1,v_2,v_3,\dots,v_{p-1}$ .其中 $v_1$ 是任意叶子节点, $v_2$ 是 $G’$ 删除 $v_1$ 后任意的叶子节点,以此类推.排序不一定唯一,但总是叶子节点在前,叶子节点总是存在,所以排序总能进行.

然后我们把 $M_0[S]$ 的行重新排序,第一行对应 $v_1$ ,第二行对应 $v_2$ $\cdots$ .之后我们对 $M_0[S]$ 的列重新排序.排序后, $e_1$ 是唯一与 $v_1$ 关联的边(因为它是叶子节点)， $\cdots$ , $e_k$ 是删除 $v_1,v_2,\dots,v_{k-1}$ 后唯一与 $v_k$ 关联的边.边的另一端在矩阵中的编号总大于这个节点,因此我们发现, $M_0[S]$ 已经变成了一个下三角矩阵,主对角线元总是 $\pm1$ ,因此我们得到 $\operatorname{det}(M_0[S]) = \pm1$.

引理证毕.

Binet-Cauchy定理设 $A,B$ 是两个 $n \times m$ 的矩阵,则有 $\operatorname{det}(AB) = \sum_S{(\operatorname{det}(A[S]))(\operatorname{det}(B[S]))}$ ,其中 $S$ 的大小为 $m$ ,且是 $\{ 1,2,\dots,m \}$ 的子集.

$A[S]$ 的记号和上面的类似,是取 $A$ 中,与 $S$ 中元素对应的 $m$ 列得到的 $m \times m$ 新矩阵;$B[S]$ 则改为取行,也得到了一个 $m \times m$ 新矩阵.

它是 $\operatorname{det}(AB) = \operatorname{det}(A) \times \operatorname{det}(B)$ (其中 $A,B$ 同阶方阵)的扩展形式.

累了不想写证明了,自己去想吧………………….

至此所有引理证明完毕.

矩阵树定理

MatrixTree定理设图 $G = (V,E)$ ,Laplace矩阵 $L$ .则 $G$ 的生成树的个数等于 $\operatorname{det}(L_0)$ ,其中 $L_0$ 是去掉 $L$ 第 $i$ 行第 $i$ 列得到的子矩阵( $i$ 任意).

证明:

不妨设去掉最后一行最后一列.

与引理1类似,我们很容易可以得到 $L_0 = M_0M_0^T$ ,这样,由 $Binet-Cauchy$ 定理可以得到:

$\operatorname{det}(L_0) = \sum_S{(\operatorname{det}(M_0[S]))(\operatorname{det}(M_0^T[S]))} \\ = \sum_S{(\operatorname{det}(M_0[S]))^2}$

而引理2告诉我们,在 $S$ 构成生成树时, $\operatorname{det}(M_0[S]) = \pm1$ ;否则等于 $0$ .因此 $\operatorname{det}(L_0)$ 就等于生成树个数.

证毕.

补充:

有 $p$ 个顶点的完全图 $K_p$ ,生成树个数为 $p^{p-2}$ 个.

可以用 $MatrixTree$ 定理来证,相信读者自证不难.

Prüfer序列也能证.

矩阵树定理的各种形式

以下内容均允许重边,但不允许自环.

无向图记号说明

设 $G$ 是一个有 $n$ 个点的无向图.
设 $# e(i,j)$ 为点 $i$ 与点 $j$ 相连的边数.
记图 $G$ 的所有生成树个数为 $t(G)$ .

有向图记号说明

设 $G$ 是一个有 $n$ 个点的有向图.
定义出度矩阵 $D^{out}(G)$ 为:

$D_{i,i}^{out} = \operatorname{deg^{out}}(i),D_{i,j}^{out} = 0,i \not = j$

类似的定义入度矩阵 $D^{in}(G)$ .
设 $# e(i,j)$ 为点 $i$ 指向点 $j$ 相连的边数.
定义出度Laplace矩阵 $L^{out}$ 为:

$L^{out}(G) = D^{out}(G)-A(G)$

定义入度Laplace矩阵 $L^{in}$ 为:

$L^{in}(G) = D^{in}(G)-A(G)$

记图 $G$ 的以 $r$ 为根的所有根向树形图个数为 $t^{root}(G,r)$ .所谓根向树形图是指，这张图的基图是一棵树,所有边全部指向父亲.

记图 $G$ 的以 $r$ 为根的所有叶向树形图个数为 $t^{leaf}(G,r)$ .所谓叶向树形图是指，这张图的基图是一棵树,所有边全部指向儿子.

矩阵树定理的各种形式

其中1,3,4用得较多.

定理1(无向图行列式形式) 对于任意的 $i$ ,都有
$t(G) = \operatorname{det}L(G) = \left(\begin{array}{cccc} 1,2,\dots,i-1,i+1,\dots,n\\ 1,2,\dots,i-1,i+1,\dots,n \end{array}\right)$

这个记号是表示第 $1,2,\dots,i-1,i+1,\dots,n$ 行,与第 $1,2,\dots,i-1,i+1,\dots,n$ 列构成的子矩阵.

定理2(无向图特征值形式) 设 $\lambda_1,\lambda_2,\dots,\lambda_{n-1}$ 为 $L(G)$ 的 $n-1$ 个非零特征值,那么有
$t(G) = \frac{1}{n} \lambda_1 \lambda_2\cdots \lambda_{n-1}$

线代没学多少,暂时不会,就留坑吧.

定理3(有向图根向形式) 对于任意的 $k$ ,都有
$t^{root}(G,k) = \operatorname{det}L^{out}(G) \left(\begin{array}{cccc} 1,2,\dots,k-1,k+1,\dots,n\\ 1,2,\dots,k-1,k+1,\dots,n \end{array}\right)$

因此如果要统计一张图所有的根向树形图,只要枚举所有的根 $k$ 并对 $t^{root}(G,k)$ 求和即可.

定理4(有向图叶向形式) 对于任意的 $k$ ,都有
$t^{leaf}(G,k) = \operatorname{det}L^{in}(G) \left(\begin{array}{cccc} 1,2,\dots,k-1,k+1,\dots,n\\ 1,2,\dots,k-1,k+1,\dots,n \end{array}\right)$

因此如果要统计一张图所有的叶向树形图,只要枚举所有的根 $k$ 并对 $t^{leaf}(G,k)$ 求和即可.

BEST定理

定理5(BEST定理) 设 $G$ 是有向图欧拉图,那么 $G$ 的不同欧拉回路总数 $ec(G)$ 是
$ec(G) = t^{root}(G,k)\prod_{v \in V}{(\operatorname{deg}(v)-1)!}$

注意,对欧拉图 $G$ 的任意两个节点 $k,k’$ ,都有 $t^{root}(G,k) = t^{root}(G,k’)$ ,且欧拉图 $G$ 的所有节点的入度和出度相等.

例题

[HEOI2015]小 Z 的房间

solution

将每个空房间看成一个节点,将相邻的可连边的点连边,注意只向下和向右连边,这样可以防止重边.得到Laplace矩阵后任意删掉第 $i$ 行第 $i$ 列后求这个行列式即可.

求行列式的方法就是高斯消元成上三角阵然后算对角线积(这题 $n$ 比较小甚至不用什么优化).

[FJOI2007]轮状病毒

solution

很直接的矩阵树定理题,麻烦的地方在于你得写高精度.

[SHOI2016]黑暗前的幻想乡

solution

考虑这题有两个限制,要一棵构成生成树,和恰好 $n-1$ 个公司建造公路.
对着图跑一遍矩阵树定理即可知道方案数,但这个答案明显多算了,所以考虑容斥.
我们计算了刚好由 $n-1$ 个公司建造的生成树个数,但是我们也统计上了刚好由 $n-2$ 个公司建造的生成树.枚举是哪 $n-2$ 个公司建造了这个树,显然这样的集合有 $\dbinom{n-1}{1}$ 种,建图的时候只加入这 $n-2$ 个公司的边,对着这个图跑一边矩阵树就可以求出方案数了对吧,然后依次减去这些集合的方案数.
但这是我们发现减多了,把刚好 $n-3$ 个公司建造的方案数多减了,所以要加回来以此类推.
同时建图是不同公司建造的相同边注意要记得加成重边.

复杂度为 $\mathcal{O}(2^{n-1}(n-1)^3 \operatorname{log}(10^9+7))$ 可以通过.

考虑加上边权会是什么样的

根据乘法原理,对于某种生成树的形态,其贡献为每条边重的次数的乘积.

如果把重边次数理解成权值的话,那么矩阵树定理求的就是:所有生成树边权乘积的总和.

(这里注意度数矩阵变成了相邻边的权值和)

[SDOI2014]重建

solution

众所周知,矩阵树求的是 $\sum\limits_{T}{\prod\limits_{e \in E}{p_e}}$

这道题求的是 $\sum\limits_{T}{(\prod\limits_{e \in E}{p_e}}\prod\limits_{e \not \in E}{(1-p_e))}$

意思是枚举每棵树, $\text{属于这个树的边出现的概率} \times \text{非树边出现的概率}$ .

$\sum_{T}{(\prod_{e \in T}{p_e}}\prod_{e \not \in T}{(1-p_e))}\\ = \sum_{T}{(\prod_{e \in T}{p_e\frac{\prod_{e}{(1-p_e)}}{\prod_{e \in T}{(1-p_e)}}})}\\ = \prod_{e}{(1-p_e)(\sum_{T}{\prod_{e \in T}{\frac{p_e}{(1-p_e)}}})}$

经典问题

考虑不是求边权积, 而是边权和.

[省选联考 2020 A 卷] 作业题

$\sum_{T}{\sum_{i=1}^{n-1}{w_{e_i}}}$

首先考虑 $w_i$ 都相同的情况, 直接套模板即可, 最后答案乘上 $w_i$ 就行.

有不同的的话, 先考虑一种暴力的做法, 枚举每一条边, 然后求出包含这条边的生成树个数.

考虑怎么更优, 一次行列式就全算出来.

把矩阵的每个位置改成一个一次函数即可, 将一条边的贡献写成 $w_i x+1$ , 最后答案就是一次项系数.

考虑答案实际上是, 钦定一条边之后的生成树个数 $\times$ 这条边的边权之和, 那么答案里被乘上一次项系数的边就是被钦定的边.

有向扩展

前面提过要任意去掉第 $k$ 行与第 $k$ 列,是因为无向图所以不用在意谁为根.

在有向树的时候需要理解为指定根,结论是:去掉哪一行就是那一个元素为根.

[CQOI2018]社交网络(外向树/叶向树)

solution

应该都能看出来是板子题.

注意以 $1$ 为根就删掉第一行第一列.

【模板】Matrix-Tree 定理

solution

还是板子题.

BEST定理

Which Dreamed It /【模板】BEST 定理

solution

BEST定理的板子题,没有代码难度,下面给出定理证明.

证明:

考虑一个内向树与一个欧拉回路的对应关系.

内向树唯一对应欧拉回路

对于点 $u (u \not= root)$ ,指定其树边出边为欧拉回路上最后从 $u$ 离开的边,而非树边按照指定顺序经过.需要证明这样的欧拉路径合法.

考虑每经过一条边就把这条边删掉,只需证明剩下的边存在欧拉路径,而有向图存在欧拉路径必须满足:

点的度数:任意点入度与出度之差都不超过1,且入度不等于出度的点最多只有两个;
弱联通性:有向边变为无向边后所有边(不是点)都在一个联通块里.

若原图符合点的限制,新图显然符合,而弱联通性需要讨论.

若删去的边是非树边 $(u,v)$ ,由于树边是每个点最后离开的边, $u,v$ 之间的树边一定还没有被删去,则 $u$ 到 $v$ 之间可以通过树边直接形成弱联通.
若删去的边是树边,则删去后 $u$ 与剩下的图完全断开,相当于删去一条链末端的边,剩下的边仍然弱联通.

点度数限制与弱连通性仍然满足,新图一定存在欧拉路径,进而说明欧拉回路满足条件.

欧拉回路对应唯一内向树

对于点 $u (u \not= root)$ ,指定其树边出边为欧拉回路上最后从 $u$ 离开的边,而非树边按照指定顺序经过.需要证明树边不成环.

假如成环

树边出边是最后离开一个点经过的边,则从树边出边离开 $u$ 后就不会再到达 $u$ ;
第一条说明从 $u$ 经过其树边出边到达 $v$ 时，$v$ 还未经过其树边出边;当 $v$ 经过其所有非树边出边后,会从其树边出边离开;
一直重复第二条的过程,会回到环上的一个点,而该点已经经过了其树边出边,与第一条矛盾.

所以树边不会成环,又由于原图 $G$ 满足欧拉回路的度数限制,所以树边构成内向树.

证毕.

补充

如果答案要求以某个点 $s$ 为起点的欧拉回路个数,那么答案是

$ans = t^{root}(G,s) \operatorname{deg}(s) \prod_{v \in V}{(\operatorname{deg}(v)-1)!}$